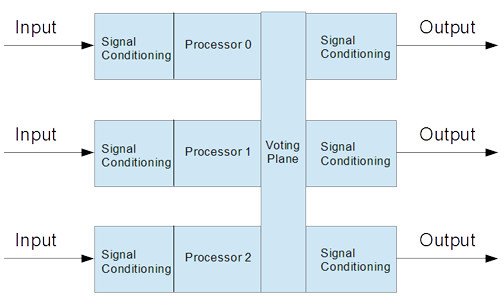
Fig. 1 – Triple Redundant Computer
Redundant Redundancy
Gerry Tyra - May 2015
Abstract:
For a safety critical system, the Gold Standard is a triple redundancy. But the engineering reality is that nothing is perfect. This paper presents the analysis of just how reliable that a KISS system would have to be to match an arbitrarily reliable triple redundant system.
Introduction:
As described elsewhere I am a proponent of Keep It Simple, Stupid (KISS) as an approach to avionics. My primary interest is in Mission Systems, and not so much in Flight Control. This has resulted in me having a more flexible approach to system timing constraints.
The basic concept behind a KISS hardware system is to have two or more computers on an aircraft sharing the computational load. But they do not replicate each others work.
If a function is time critical, there is a primary process to execute that function, with a backup copy “sleeping” on another computer. If the critical function fails, for whatever reason, the backup is signaled to wake up. For less critical functions, a replacement processes can be loaded and initialized.
The other day, I was asked, “How does KISS reliability compare to a triple redundant system?”
To be honest, I didn't have a clue. So, I started doing the analysis that follows.
Flexibility as a Virtue:
I consider flexibility to be a critical feature of any robust computer system. As such, a triplex redundant system is the opposite. The foundation of a redundant system is that identical functionality occurs simultaneously in three+ computers and the results are presented to a voting plane in a unified and coherent manner. That is pretty rigid. There is very little allowance to go in and “tweak” a function or add new functionality. It can be done, but re-certification will probably be a significant effort.
This rigidity of a triplex redundant systems is one of its major costs. So, if KISS is competitive in reliability, there are a major cost and performance savings possible from switch in system architectures.
Problem Space:
Engineers always fight the specter of failure. Planes crash, ships sink, cars collide. Entropy happens.
Part of the Art of Engineering is to build things that perform their function safely and reliably. “Safe” is defined as the system working without a failure, for some period of time, to some probability. For this paper, the benchmark is an aircraft computer system on a 10 hour mission, with a probability of success of .99999 (i.e. five 9s, which is one failure per 1 million flight hours).
For a triple redundant computer to meet this specification, the Mean Time Between Failures (MTBF) of the each computer in the system can be calculated. If any candidate computer for the design has a MTBF below this value, either that computer should not be used, or additional precautions have to be added to the design.
But, triple redundancy comes at a cost in hardware and software. So, the question is asked: What is the computer reliability, measured as MTBF, required of a avionics suit designed in line with KISS to obtain the same 10 hour, five 9s reliability?
Caveat Emptor:
What follows is a SWAG (for the uninitiated: Scientific Wild Ass Guess). It is meant as a first order estimate to determine if a KISS system can reach an arbitrarily level of reliability. By no stretch of the imagination should this be taken as a comprehensive analysis. Assumptions will be identified as appropriate.
Hardware, Then, Now and in the Future:
In my youth, wire wrapped boards were a fairly common implementation. There was a forest of antennas transmitting at the clock frequency of the card. Printed circuit cards were also available, but they problems with delamination and cold solder joints. But years of development, improved materials and processes, more layers, better trace patterns with one or more solid ground planes have brought us a long way.
Add in greater levels of integration and the performance per square inch of a card is rather phenomenal.
But life is still not perfect. The “bathtub curve” is real. Once you get through the infant mortality portion of the life cycle, you enter a (hopefully) extended period of low rate random failures. And that rate is nearly constant over the “bottom” of the curve. Eventually, old age catches up and the failure rate starts to increase.
What better engineering, greater integration and tight quality control have brought us is a lower failure rate at the bottom of the tub for a longer period.
One important note that frequently gets lost in the noise: The component in the 10th percentile of the “random” period at the bottom of the tub is no more reliable than a part at the 70th percentile. Swapping out all the components that reach the 50th percentile with new components does NOT improve system reliability. Swapping at the 50th percentile just increases your maintenance cost by 100% without measurable improvement in reliability. Swapping at the 95th percentile, just before the aging cycle kicks in, works just as well and is a lot cheaper over the life of a fleet.
All of this being said, hardware is the source of all random errors. There is noise in all of the components. When that noise exceeds the threshold, be causes an error. When a component burns out, or a solder joint opens, permanently or intermittently, it causes an error. Some errors are transient, such as an ionizing particle passing through a DRAM memory cell. Other errors are what is left as the computer becomes a smoking hole in the air-frame.
Assumption: all hardware failures will be treated as permanent. The differentiation of failure modes and their relative probabilities is a major effort for a fully specified system, and is well beyond this paper.
Software – Magic vs. Science:
As another test case goes sideways, I have been known to cry out, “I Hate MAGIC!”
That's what it frequently feels like. Some uncontrollable force is arbitrarily redirecting my perfect software into strange and arcane parts of memory.
No such luck. It's just another subtle bug, that I put in, that only kicks in under the “right” circumstances.
Software is, by definition, deterministic. However, as programs become more complex, the dimensions of the state machine representing that program become enormous, with lots of hiding places for obscure bugs to lay in wait. So, even testing as much as you can, there will usually be an edge case or two that wasn't fully tested.
Here, unfortunately, is one of the frequently unaddressed issues with triple+ redundant systems, the software error. If all three computers are running the same software, and are given the same inputs, they will all reach the same error state together and …
Well, it depends. If the system detects the error and does something like throw an exception, the system will do a partial or complete reset. In most avionics systems is is not good, but it usually isn't lethal either. What can be really ugly is if this error escapes and starts commanding actions in the aircraft. After all, all three computers said that the next command was correct.
It is possible to independently write functionally identical software for each computer in a triplex system. Once upon a time, when computers were smaller and slower, and the complexity of the software was much lower, this could be done. But in a system with millions of line of code, the cost of three independent software development efforts, and the issues of Configuration Management of that code, is well beyond prohibitive.
Assumption, the KISS design has a potential advantage here. If the error is detected via an exception or a bounds violation, either internally or at the Remote Interface Unit (RIU, but more on this later), the offending process can be shut down, a hot standby copy released to take up the work, and the original process restarted as the standby. There are a lot of assumptions here about the time constants that divide a “glitch” that can be recovered from an error that will result in a crash. More on this later. But, again, the true analysis exceeds the scope of this paper.
We are left with potentially buggy software, that may, or may not lock up the system. And at this level of analysis, there is no objective way of quantifying the impact of the software on reliability. So, we move on and analysis what we can.
Classic Triplex:
First, the simple case: A triplex system with all of the signal conditioning contained in each of the three systems. There are analog and discrete signals coming in, the result is computed in each processor. A voting mechanism is provided to keep a wayward computer from disrupting the output. Then the analog and discrete outputs are generated.

Fig.
1 – Triple Redundant Computer
This implementation has two drawbacks in my opinion and both are related to the complexity of implementation. The first is the implementation of the voting planes. The questions is: How is the plane implemented without creating a new single point of failure. If the voting planes are redundant, how how do the planes vote against each other. The problem takes on a recursive element that requires very careful design and analysis to resolve.
A related issue is re-synchronizing a processor that has had a transient upset. The problem lies in the algorithms used by the system. If the algorithms use methods like Finite Impulse Response filters, the stray computer should come back into synchronization with the other two. However, if the equivalents of Infinite Impulse Response filters are used, the dependency on previous state data may make it impossible to re-synchronize the overall system without a master reset.
Having said that, let's calculate the reliability of the individual computers making up the systems.
In a triple redundant system, “success” is to complete the mission with two or three computer working. The probability of a single computer working for the mission is Ri (i=0...2). The full system probability, Rs, of all three computers working is Ri3. The probability of Rs with only one computer out is 3Ri2(1-Ri). Simplifying, the result is:
.99999 = 3R2 - 2R3
So, the 10 hour per computer reliability has to be .9985, or .99985 per hour.
Reliability = e -time/MTBF or MTBF = -1/ln(Reliability)
Therefore, a computer with a MTBF of 666 hrs will meet the reliability requirement. This will serve as our baseline.
Distributed Triplex:
In this system, the I/O functionality is handled remotely by Remote Interface Units (RIUs). The RIUs are connected to the triplex computers via some form of network. The RIU moves the signal conditioning closer to the sensor or actuator that is under control. This reduces noise in the sensors, and mass in the wiring harness. Given a system on a chip implementation, the RIU can easily handle any common network protocol and serve as a final error check against predefined signal bounds.
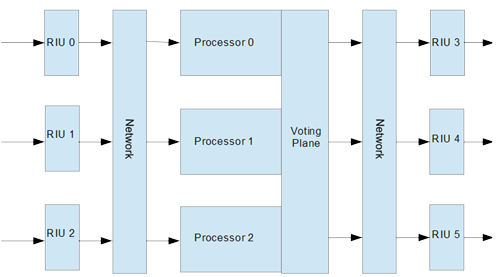
Fig.
2 Distributed Triple Redundant Computer
Assumption: In a classic triplex, there is a lot of wiring going into the system and then out again. Then there is the complexity of the signal conditioning elements in each of the member computers of the triplex. The assumption is that moving to RIUs does not adversely impact reliability and that the previously calculated MTBF is still valid.
Assumption: The reliability of a given computer from input to output is serial. The simplifying assumption is that the reliability of the actual computer and the net value for the RIU w/network in the distributed triplex system are the same.
Therefore:
Reliabilitycomputer = 3√.99985 = .99995 => MTBF = 20,000hr
A MTBF of 20,000 hrs is well within the fielded range for mobile computer systems, where 30K to 70K hrs is common. Fixed base computers can have much higher reliability, because of a more benign environment, but no one said avionics computers worked in a benign environment.
We now have a working value for a 10hr mission with which to measure a comparably distributed KISS system.
KISS Reliability:
Assumption: This is a big one, that either the actual running program, a supervisory program or an out of bounds value at an RIU will flag the fault soon enough. In most cases, this isn't too hard to have happen. But it is not the immediate, knee jerk, response that a triplex system provides. Most aircraft won't depart in less than a couple seconds. So, if the transition to the backup can be made in less than a half a second, or better a tenth, the assumption can stand. If, on the other hand, we are talking about the vector control of a large engine, the time may not be available.
What this assumption really says is that you have to analyze the target system and determine the critical time frames, the time to detect a fault, the time to switch and the time to recover. But for the moment, we are accepting this assumption just to evaluate the underlying hardware reliability.
Assumption: The individual computers in the KISS system have enough reserve throughput and memory to be able to run the additional processes imposed by a failure in another computer. If your design is running all the processors at 80% capacity, this assumption fails.
We will not be taking into account the potential improvement in reliability by removing the voting planes, the ease of restarting a system that has had a transient failure, or the problems with re-synchronizing a running process. This is meant to only be a head to head hardware comparison.

Fig.
3 KISS System
Going back to the beginning, we are looking for .99999 reliability on a 10 hour flight. We have two computers talking to RIUs. If one computer is running, the mission continues. There are four cases, both work, one or the other works, neither works. So the probability of mission success is:
Rs = Ri2 + 2Ri(1-Ri) = 2Ri - Ri2
This provides a one hour value of Ri = .9969. Or .99969 for 10 hours. This yields as a minimum, MTBF = 3225 hrs. But, this value is from input, through computation and then output.
Given that we have already accepted that the RIUs and network have a reliability of .99995, we can calculate the computer's reliability as:
Ri = RcRRIU2 => Rc = .99979 => MTBF = 4761 hrs.
Or to put it another way, the KISS proccessor needs to be only 1/4th as reliable as a triple redundant computer to obtain the same level of system reliability.
Working Backwards:
Another question is: What reliability is obtained by using the 20,000 MTBF computers required by the second case? This sets Ri = .99985, so the system reliability Rs = .9999999775 per hour. This means that the system MTBF = 44,444,444 hrs.
Summary:
This paper has shown that a KISS oriented system could be built, given certain conditions, that is more reliable than a triple redundant system. And this is accomplished without the complexity of voting planes, simultaneous failures in software or trying to re-synchronize after a transient fault.
We have just gone through a lot of assumptions, and used an arbitrary performance criteria. The author was as surprised by the result as the reader probably was. This paper is not the final answer. If you are building a safety critical system, what this paper has shown is that a KISS system should at least be considered before arbitrarily going with a triplex system.